PAM Representation of GMSK and Serial Receivers

1. Abstract

This report is on Laurent Representation (a.k.a. PAM representation) of GMSK. According to Laurent, a CPM signal can be written as sum of several PAM signals. Laurent's representation of CPM signals resembles Fourier decomposition in many ways. This approach enables many different receiver types, most notably the serial receiver, which is found by Kaleh.

You can find sample MATLAB codes here.

2. Introduction

GMSK waveform is a CPM scheme and can be modeled as sum of several PAM waveforms [1]. Luarent's representation enabled two new receivers for CPM signals, especially for GMSK [2, 3]. First one is a Viterbi Algorithm type of receiver and the second one is a serial receiver. Since there are other, easier to understand and implement Viterbi Algorithm receivers for GMSK, this one is not further investigated in this report. However, the computation cost of the serial receiver is very low, which is why this report is written.

In the following section, mathematical background of PAM representation of CPM is further investigated. After that a sample problem is solved for a specific case for further clarification of the subject. Next, some remarks are reiterated for clarification of PAM representation. Finally, the serial receiver is implemented and simulation results are presented.

3. PAM Representation of CPM

A CPM signal has the following form [4]:

s(t, \underline{\alpha}) = \sqrt{\frac{E}{T}}exp\{j\psi(t, \underline{\alpha})\},

where E is the symbol energy, T is the symbol duration and \underline{\alpha} is a sequence of bipolar NRZ symbols. \psi(t, \underline{\alpha}) is defined as follows:

\psi(t, \underline{\alpha}) = \pi h\sum_{i=0}^{n} \alpha_i q(t-iT), \quad nT \leq t < (n+1)T.
Here, h is the modulation index and is always 0.5 for MSK signals. q(\cdot) is the so called phase shaping filter:

q(t) =
\begin{cases}
0, & t < 0, \\ \int_{0}^{t}f(\tau)d\tau, & 0 \leq t < LT,\\ 1, & t \geq LT \end{cases}
where f(\cdot) is the frequency shaping filter. It is defined as follows:

f(t) = \frac{1}{2T}\bigg[Q(2\pi B \frac{t-\frac{T}{2}}{\sqrt{ln(2)}}) - Q(2\pi B \frac{t+\frac{T}{2}}{\sqrt{ln(2)}})\bigg],

where B = BT/T, with BT the so called time bandwidth product Q(\cdot) is the famous Q function.

Laurent rewrote Eq. eq:cpm_sig}:

s(t, \underline{\alpha}) = \sqrt{E}\sum_{k=0}^{2^{L-1}} \sum_{i=0}^{n-1} a_{k,n} h_k(t-nT),

where L is the extent of the phase shaping function as in Eq. eq:phase_shaping, a_{k,n} are the so called auxiliary symbols. Finally h_k(\cdot) is the PAM signal and is different from the modulation index h.

In order to formulate h_k(\cdot) Luarent started with two auxiliary equations [1]:

J \triangleq e^{jh\pi},

and

c(t) \triangleq \begin{cases}
\frac{sin(\pi h - \pi h q(t))}{sin(\pi h)}, & 0 \leq t < LT, \\ c(-t), & -LT < t \leq 0, \\ 0, & o.w. \end{cases}
with h being the modulation index in both equations. Then the exponential part in Eq. eq:cpm_sig is rewritten as follows:

exp\{j\psi(t, \underline{\alpha})\} = exp\bigg\{j\pi h\sum_{i=0}^{n-L} \alpha_i \bigg\} \prod_{i=n-L+1}^{n} exp\big\{j\pi h\alpha_i q(t-nT)\big\}.

This is very much like the Trellis like representation in [5]. Since for MSK, h=0.5, Eq. eq:c_long can be simplified as follows:

c(t) \triangleq \begin{cases}
cos\Big(\frac{\pi q(t)}{2}\Big), & 0 \leq t < LT, \\ c(-t), & -LT < t \leq 0, \\ 0, & o.w. \end{cases}
In addition to this, in MSK \alpha_i are bipolar NRZ, s.t. \alpha_i \in \{\pm1\}. Thus J^{\alpha_i} = cos(\pi h) + j\alpha_i sin(\pi h). This is a direct consequence of \alpha_i being bipolar NRZ.

The product term in Eq. eq:rewrite becomes:

exp\big\{j\pi h\alpha_i q(t-nT)\big\} = cos\big(\pi h\alpha_i q(t-nT)\big) +jsin\big(\pi h\alpha_i q(t-nT)\big),

which is equal to,

exp\big\{j\pi h\alpha_i q(t-nT)\big\} = \frac{sin\big(\pi h - \pi h q(t-nT)\big)}{sin(\pi h)} +J^{\alpha_i}\frac{sin\big(\pi h q(t-nT)\big)}{sin(\pi h)}.

Due to the properties of the Gaussian function q(\cdot) in Eq. eq:phase_shaping,

1-q(t) = q(LT) - q(t) = q(LT-t),

also using Eq. eq:c_long, following can be written,

\frac{sin\big(\pi h q(t)\big)}{sin(\pi h)} = c(t-LT).

All these definitions enable us to rewrite Eq. eq:cpm_sig as follows:

s(t, \underline{\alpha}) = \sqrt{\frac{E}{T}} a_{0,n-L} \prod_{i=n-L+1}^{n} \bigg[J^{\alpha_i}c(t-nT-LT) + c(t-nT)\bigg].

Here a_{0, i} are complex symbols and are related to the actual symbols \alpha_i as follows:

a_{0,n} = exp\bigg\{j\pi h\sum_{i=0}^{n} \alpha_i \bigg\} = a_{0, n-1}J^{\alpha_n} = a_{0, n-2}J^{\alpha_n}J^{\alpha_{n-1}}.


In Eq. eq:pam_1, only the most recent L symbols contribute to the transient part of the equation where as previous symbols from 0 to n-L have constant effect. This is essentially very similar to the Trellis representation of CPM. After the product term in Eq. eq:pam_1 for a particular L is expended, the CPM function becomes summation of several varying c(\cdot) functions. This new representation is the so called PAM representation of CPM. An example expansion of the product term for L=3 is solved in the next chapter which will make everything much more clear.

4. Example Solution for L=3

In order to fully visualize how PAM representation works, in this chapter a sample problem for L=3 is solved. For L=3 Eq. eq:pam_1 turns into the following:

s(t, \underline{\alpha}) = \sqrt{\frac{E}{T}} a_{0,n-3} \prod_{i=0}^{2} \bigg[J^{\alpha_i}c(t-iT-3T) + c(t-iT)\bigg].

Here, the product term is over 0,1,2 after some rearrangement of terms. The product term is then expanded as follows:

\begin{aligned}
s(t, \underline{\alpha}) = \sqrt{\frac{E}{T}} a_{0,n-3} \Bigg[ & \bigg(J^{\alpha_{n}}c(t-nT-3T) + c(t-nT)\bigg) \\ & +\bigg(J^{\alpha_{n-1}}c(t-nT-2T) + c(t-nT+T)\bigg) \\ & +\bigg(J^{\alpha_{n-2}}c(t-nT-T) + c(t-nT+2T)\bigg)\Bigg]
\end{aligned}

then multiplying all these terms result in:

\small
\begin{aligned}
s(t, \underline{\alpha}) = & \sqrt{\frac{E}{T}} a_{0,n-3} \\ &
\Bigg[ \bigg(J^{\alpha_{n}}J^{\alpha_{n-1}}J^{\alpha_{n-2}}c(t-nT-3T)c(t-nT-2T)c(t-nT-T)\bigg) \\ & +\bigg(J^{\alpha_{n}}J^{\alpha_{n-1}}c(t-nT-3T)c(t-nT-2T)c(t-nT+2T)\bigg) \\
& +\bigg(J^{\alpha_{n}}J^{\alpha_{n-2}}c(t-nT-3T)c(t-nT+T)c(t-nT-T)\bigg) \\
& +\bigg(J^{\alpha_{n}}c(t-nT-3T)c(t-nT+T)c(t-nT+2T)\bigg) \\
& +\bigg(J^{\alpha_{n-1}}J^{\alpha_{n-2}}c(t-nT-2T)c(t-nT)c(t-nT-T)\bigg)\\
& +\bigg(J^{\alpha_{n-1}}c(t-nT-2T)c(t-nT)c(t-nT+2T)\bigg)\\
& +\bigg(J^{\alpha_{n-2}}c(t-nT)c(t-nT+T)c(t-nT-T)\bigg)\\
& +\bigg(c(t-nT)c(t-nT+T)c(t-nT+2T)\bigg)\Bigg]
\end{aligned}

Next, a_{0,n-3} is distributed into the whole multiplication combined with the definition in Eq. eq:a_0_n results in the following 8 multiplication of c(\cdot) functions grouped in their respective auxiliary symbols:

\begin{aligned}
& a_{0,n}c(t-nT-3T)c(t-nt-2T)c(t-nT-T) \\
& a_{0,n-1}c(t-nT-2T)c(t-nt-T)c(t-nT) \\
& a_{0,n-2}c(t-nT-3T)c(t-nt-2T)c(t-nT-T) \\
& a_{0,n-3}c(t-nT)c(t-nt+T)c(t-nT+2T) \\
\end{aligned}


\begin{aligned}
& a_{1,n}c(t-nT-3T)c(t-nt-T)c(t-nT+T) \\
& a_{1,n-1}c(t-nT-2T)c(t-nt)c(t-nT+2T) \\
\end{aligned}


\begin{aligned}
& a_{2,n}c(t-nT-3T)c(t-nt-2T)c(t-nT+2T) \\
\end{aligned}


\begin{aligned}
& a_{3,n}c(t-nT-3T)c(t-nt+T)c(t-nT+2T) \\
\end{aligned}

After a_{0,n-3} is distributed, is can be seen that the main auxiliary symbol a_{0,n-i} has 4 c(\cdot) sequences associated with it. This is natural since it is expected that the main auxiliary symbol to have the most energy within it as previously shown in the PAM signals. Next, a_{1,n-i} has the second most energy as expected and so on. Next step is to generate a set of h_k(\cdot) so that these 4 set of functions are gathered together, which is not so hard:

\begin{aligned}
s(t, \underline{\alpha}) = & \sqrt{\frac{E}{T}}
\Bigg[a_{0,n} h_0(t-nT) + a_{0,n-1}h_0(t-nT+T) \\
& + a_{0,n-2}h_0(t-nT+2T) + a_{0,n-3}h_0(t-nT+3T) \\
& + a_{1,n}h_1(t-nT) + a_{1,n-1}h_1(t-nT+T) \\
& + a_{2,n}h_1(t-nT) + a_{3,n-1}h_1(t-nT) \Bigg]
\end{aligned}

with

\begin{aligned}
& h_0(t) = c(t-3T)c(t-2T)c(t-T) \\
& h_1(t) = c(t-3T)c(t-T)c(t+T) \\
& h_2(t) = c(t-3T)c(t-2T)c(t+2T) \\
& h_3(t) = c(t-3T)c(t+T)c(t+2T) \\
\end{aligned}

and c(\cdot) function is as defined in Eq. eq:c_long. Considering this example, h_k(t) functions have the following form in Fig. [1]. In this figure, the CPM scheme is considered to be GMSK with BT=0.3. In [2], another solution for L=4 is also given as a comparison.

Figure 1. PAM curves for L=3 case for GMSK.

5. Some Important Remarks on PAM Representation of CPM

In the previous chapter the CPM signal is written as summation of several PAM signals for L=3 case. The original bipolar NRZ symbols are mapped to complex auxiliary symbols.

However, the auxiliary symbols that belong to a particular h_k(t) has differential encoding type of relation. This is a very important observation since it means that PAM representation of CPM scheme has an inherent differential encoding embedded within. This has to be taken care in the transceiver duo either in the receiver or the transmitter. Differential encoding is a popular method for non-coherent reception.

Thus, if PAM representation is considered at the receiver without doing anything at the transmitter, then the inherent differential encoding structure has to be differentially decoded at the receiver in order to go back to the original symbols. This also automatically means the receiver is non-coherent.

If a differential decoder is employed at the transmitter chain, then together with the inherent differential decoding of PAM representation at the receiver will yield net result of no encoding-decoding. This is because the symbols are pre-decoded at the transmitter and encoding them back due to PAM representation results in original symbols, which automatically resulting with the coherent receiver.

6. Serial Receiver

Serial receiver is developed according to the inherent differential encoding. As mentioned earlier, there are two receiver types, (a) coherent, (b) noncoherent. For all cases though, the received signal has the following form:

z(t) = s(t, \underline{\alpha}) + n(t),

where s(t, \underline{\alpha}) is as in Eq. eq:cpm_pam and n(t) is additive white Gaussian noise. If receiver is based on the PAM representation, naturally the optimum receiver has to be a filter bank that is matched to the respective h_k(t) functions.

Now, lets assume that there is a hypothetical sequence of auxiliary symbols \hat{a}_{0,n}, which maximizes the following metric:

\begin{aligned}
\Lambda & = Re\Bigg\{\int_{-\infty}^{\infty} z(t)\sum_{i=0}\hat{a}^*_{0,i}h_0(t-iT)dt \Bigg\} = Re\bigg\{\sum_{i=0}\hat{a}^*_{0,i} r_{0,i}\bigg\} \\
& = \sum_{i=0}a_{0,2i}Re \big\{r_{0, 2i} \big\} + Im \bigg\{\sum_{i=0}a_{0,2i+1}\bigg\} Im \big\{r_{0, 2i+1} \big\}
\end{aligned}

with,

r_{0,i} = \int_{-\infty}^{\infty} z(t)h_0(t-iT)dt.

This is basically the maximum likelihood sequence detection (MLSD) receiver and is the optimum one. Eq. eq:optimum_receiver also implies that the necessary statistics required are the real parts of 2i samples and imaginary parts of 2i+1 samples, which enables the so called linear receiver [2].

This idea is logical since if the GMSK is received using PAM representation, original bipolar NRZ symbols are encoded into complex auxiliary symbols. Complex auxiliary symbols follow a simple differential encoding scheme which encodes the original symbols into other \pm 1 for even samples and \pm j for odd samples.

Next, for the serial receiver, we can make some further assumptions. Lets continue with the previous L=3 case for GMSK as an example. There are 2^{L-1} = 4 PAM functions as previously shown. 2 of these, h_2(t) and h_3(t) has virtually no energy in them compared to h_0(t) and h_1(t). Here, in [2, 3] it is assumed that h_1(t) component enhances the noise. Since auxiliary symbols that belong to different PAM components are all mutually uncorrelated, the Wiener filter only tries to reduce the effect of noise. In this report, a different (and possibly novel) approach is taken.

First, the following equation is written again:

z(t) = \sqrt{E}\sum_{i=0}^{n-1}\bigg[a_{0,i}h_0(t-iT) + a_{1, i}h_1(t-iT)\bigg] + n(t).

This approximated signal is then passed through h_0(-t):

\small
\begin{aligned}
z(t) & \ast h_0(-t) =\Bigg[\sqrt{E}\sum_{i=0}^{n-1}\bigg[a_{0,i}h_0(t-iT) + a_{1, i}h_1(t-iT)\bigg] + n(t)\Bigg] \ast h_0(-t) \\
& = \sqrt{E}\sum_{i=0}^{n-1}\bigg[a_{0,i}h_0(t-iT)\ast h_0(-t) + a_{1, i}h_1(t-iT)\ast h_0(-t)\bigg] + n(t)\ast h_0(-t)
\end{aligned}

Here, the following definitions are made in order to simplify the above equation,

\begin{aligned}
& r_{00}(t) = h_0(t-iT)\ast h_0(-t), \\
& r_{10}(t) = h_1(t-iT)\ast h_0(-t), \\
& n_{0}(t) = n(t)\ast h_0(-t), \\
\end{aligned}

r_{00}(t) is the auto-correlation of h_0(t) with itself, r_{10}(t) is the cross correlation of h_0(t) and h_(t) and n_0(t) is the filtered noise.

Since the primary PAM component has the most energy in it, expectation is that auxiliary symbol a_{0,i} will be extracted. However, h_0(t) and h_1(t) are not exactly orthogonal as it would be in an ordinary communication scheme. Thus, some left over auxiliary symbols from the second PAM component will leak into the primary auxiliary symbols. This leak is called co-symbol interference (CSI) for the remainder of this report. This effect is in addition to the inter-symbol interference (ISI) of general GMSK scheme.

The CSI can be considered as a colored noise since in [2], it is shown that different auxiliary symbols that correspond to different PAM components are mutually uncorrelated. Thus serial reception with h_0(-t) filter extracts the a_{0,i} auxiliary symbols but enhances the overall noise as well.

Because of this, in [2], Kaleh employed a Wiener filter in order to minimize the effect of this additional term. However, Wiener filtering requires a good idea on the noise variance (hence SNR) in order to work properly. Thus, a different take on the Wiener filter applied in this report.

Lets assume that there is a filter h_{opt}(t) such that:

\begin{aligned}
& h_0(t-iT) \ast h_{opt}(-t) = \delta[iT], \\
& h_1(t-iT) \ast h_{opt}(-t) = 0, \\
\end{aligned}

so that correlation of the filter with h_0(t) at time iT is a Dirac delta function and correlation of the filter with h_1(t) is zero. Such a filter than should eliminate all the CSI from second PAM component. Moving on, lets assume some coefficients c[k] such that,

h_0(t) + h_1(t) = \sum_k c[k] h_{opt}(t-kT).

Right hand side of this equation is essentially a convolution as well.

Next, both sides of the equation are matched filtered with h_0(t):

h_0(-t)\ast \bigg[h_0(t) + h_1(t)\bigg] = h_0(-t)\ast \bigg[\sum_k c[k] h_{opt}(t-kT)\bigg],

and using the identities in Eq. eq:identities, the following can be written:

r_{00}(t) + r_{10}(t) = \sum_k c[k].

Putting this equality inside Eq. eq:coeff_eq, the optimum filter h_{opt}(t) can be found as follows:

h_0(t) + h_1(t) = \bigg[r_{00}(t) + r_{10}(t)\bigg]\ast h_{opt}(t-kT).

Taking the Fourier transform and then solving in the frequency domain and finally taking the inverse Fourier transform is an easier to solve for this filter. One important note is that \sum_k c[k] h_{opt}(t-kT), is convolution of a discrete filter and h_{opt}(t) sampled at times kT. Thus naturally c[k] discrete filter is in symbol domain rather than sample domain. This is important because there are 2 methods to apply the optimum filter:

1. h_{opt}(t) can be computed and directly applied instead of h_0(t) in sample domain, this filter would have more coefficients in total compared to h_0(t),
2. c[k] can be computed and applied after h_0(t) and a sampling block, h_00(t) and c[k] would both have much less coefficients in total compared to h_{opt}(t)

Thus depending on the capabilities of the designed system, both options are viable and realizable. Another important property of the c[k] filter is that, it will approach to \delta [k] as BT \gg 1. This is due to the PAM components other than h_0(t) all start to diminish even at low values of BT such as BT = 0.5.

The following 4 receivers are the possible coherent and non-coherent receivers with different applications of the optimum filter.

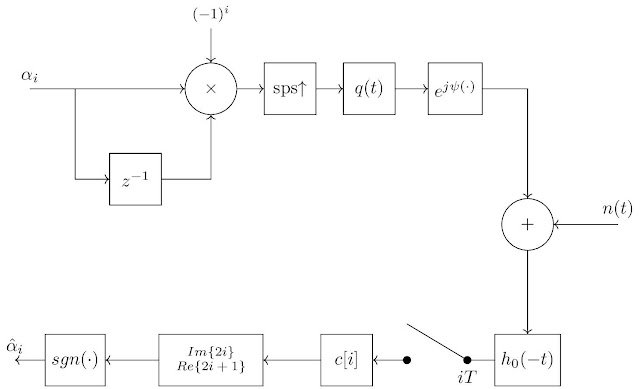
7. Serial Coherent Receiver

Since PAM reception inherently employs differential encoding, in order to coherently receive with PAM representation, a differential decoder has to be employed at the beginning of transmitter [6, 2]. This differential decoder breaks the inherent differential encoding of the PAM representation, thus the received symbols in PAM representation become directly the original symbols. The block diagram of the coherent transmitter-receiver is in Fig. 2.

Figure 2. Coherent transmitter-receiver block diagram.

8. Serial Noncoherent Receiver

Previously, it is mentioned that the auxiliary symbols that belong to different PAM component are mutually uncorrelated. However, the same is not the case for the symbols that belong to the same PAM component. The relationship between the original symbols and auxiliary symbols are given in Eq. eq:a_0_n. Naturally, the auxiliary symbols are correlated to each other.

In [3], a method is given to weaken the correlation between the consecutive auxiliary symbols, which should increase the overall BER performance. The idea is basically to increase the depth of differential encoding additionally by employing a complex differential encoder.

A new parameter M is introduced as an odd number, which stands for the total differential encoding depth of the system. The complex differential encoder is as follows:

\beta_i = (-1)^{\frac{M-1}{2}}\alpha_i \prod_{n=1}^{M-1}\beta_{n-1},

Thus M=7 means a complex differential encoder of depth 6 is employed before generating the auxiliary bits and creating the baseband signal. With the addition of the auxiliary bit generation, the total differential encoding depth of the system becomes 7. As a side note, M=1 means no extra differential encoding is done and just PAM receptions inherent differential encoding is present.

In [3], receiver for only odd numbers of M is given. For even M, the decision metric becomes much more complex and is not further explored. Details of the optimum receiver and its decision is also shown there and is not rewritten here.

Since there is differential encoding in the system, this has to be differentially decoded in order to reach the original symbols at the receiver. The total depth of the differential decoder is M.

The block diagram of the transmitter and receiver is in Fig. 3. Here, differential decoder works on the complex signal where as the encoder's input is bipolar NRZ symbols. The gain block only applies -1 or 1, in fact for odd M which is the case in this report and in [3], gain block simply has no effect.

Figure 3. Noncoherent transmitter-receiver block diagram.

9. Conclusion

The corresponding BER curves for various other GMSK receivers and some BPSK receivers is shown in Fig. 4. In the figure, BT = 0.3, M=7, L=3 and K = 30, where K stands for the number of Wiener filter coefficients. As expected, coherent serial receiver, approaches to the BPSK. This is because, PAM representation of GMSK is simply a BSPK type of receiver with some ISI and CSI. As BT increases, both ISI and CSI will diminsh and GMSK will in fact perform as good as BPSK. This can be seen in Fig. 5 where BT=0.5.

Figure 4. Performance of various GMSK schemes for BT = 0.3.

Figure 5. Performance of various GMSK schemes for BT = 0.5.

10. References

[1] Pierre Laurent. Exact and approximate construction of digital phase modulations by superposition of amplitude modulated pulses (amp). IEEE transactions on communications, 34(2):150–160, 1986.
[2] Ghassan Kawas Kaleh. Simple coherent receivers for partial response continuous phase modulation. IEEE Journal on Selected Areas in Communications, 7(9):1427–1436, 1989.
[3] Ghassan Kawas Kaleh. Differentially coherent detection of binary partial response continuous phase modulation with index 0.5. IEEE transactions on communications, 39(9):1335–1340, 1991.
[4] John B Anderson, Tor Aulin, and Carl-Erik Sundberg. Digital phase modulation. Springer Science & Business Media, 2013.
[5] Musa Tunç Arslan. Maximum likelihood sequence detector for gmsk. Technical report, Meteksan Defence Inc., 2018.
[6] Gee L Lui. Threshold detection performance of gmsk signal with bt= 0.5. In Military Communications Conference, 1998. MILCOM 98. Proceedings., IEEE, volume 2, pages 515–519. IEEE, 1998.